반응형
선택 문제 (Selection Problem)
- n 개의 숫자들 중 k 번째로 작은 숫자를 찾는 문제
간단한 idea
- 최소 숫자를 k번 찾는다
- O(kn)
- 숫자들을 정렬한 후 k번째 숫자를 찾는다
- O(nlogn)
Idea
이진 탐색 (Binary Search)
- 정렬된 입력인 경우, 중간에 있는 숫자와 찾고자 하는 숫자를 비교함으로써, 입력을 반으로 나눈 두 부분 중 한 부분만을 검색
선택 문제
- 입력이 정렬되지 않는 형태, 입력 숫자 중 피봇을 선택하여 분할

Pseudo code
- Selection(A, left, right, k)
- Input: A[left] ~ A[right]와 k, 단 1 ≤ k ≤ |A|, |A| = right - left + 1
- Output: A[left] ~ A[right]에서 k 번째 작은 원소
1. 피봇을 A[left] ~ A[right]에서 랜덤하게 선택
2. 피봇과 A[left] 변경
3. 피봇과 배열의 각 원소와 비교하여 피봇보다 작은 숫자는 A[left] ~ A[p - 1]로 옮기고,
피봇보다 큰 숫자는 A[p + 1] ~ A[right]로 옮기고 피봇은 A[p]에 놓는다. (partition)
4. S = (p - 1) - left + 1 // S = Small Group의 크기
5. if (k <= S) Selection(A, left, p - 1, k) // Small Group에서 찾기
6. else if (k = S + 1) return A[p] // 피봇 = k번째 작은 숫자
7. else Selection(A, p + 1, right, k - S - 1) // Large group에서 찾기고려사항
- 해당 알고리즘은 분할 정복이면서 랜덤 알고리즘
- 피봇을 랜덤하게 정하기 때문
- 피봇을 너무 한쪽으로 치우치게 분할하면 수행시간이 길어짐
- Small group.size << Large group.size || Small group.size >> Large group.size
- 위 경우 수행시간이 길어짐
- 한쪽으로 치우치게 분할될 확률은 동전을 던질 때 한쪽 면이 나오는 확률과 같음
good / bad 분할
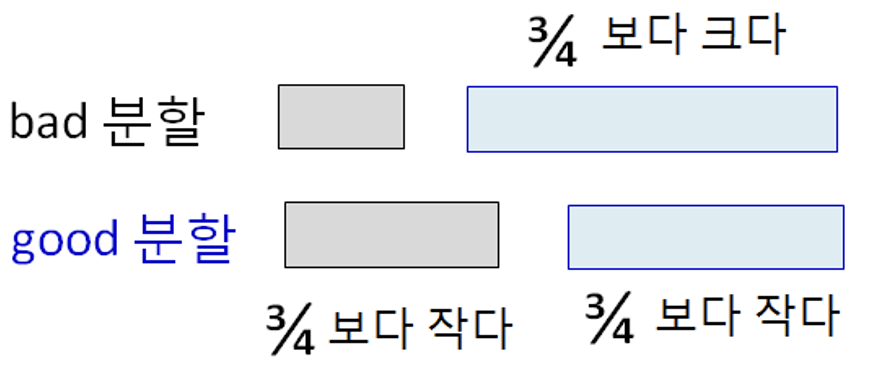
Example
- A = intArrayOf(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16)
- 위 A 배열에서 5 ~ 12 중 하나가 pivot이 될 경우 good 분할
- 반대로 1 ~ 4, 13 ~ 16 중 하나의 경우 bad 분할
- 따라서, 확률은 동일하다
Time Complexity
- 배열의 크기가 n에서부터 3/4배씩 감소
- 배열의 크기가 1일 때는 분할 불가
- O(n + 3/4 n + (3/4)^2 n + …… + (3/4)^i n) = O(n)
- 평균 2번 만에 good 분할이 되므로 2 * O(n) = O(n)
- 따라서 O(n)이다.
응용
- 데이터 분석을 위한 중앙 값 (median)을 찾는 데 활용
Example
private class SelectionExample {
fun solution(nums: IntArray, k: Int): Int = selection(a = nums, k = k)
private fun selection(
a: IntArray,
k: Int,
left: Int = 0,
right: Int = a.lastIndex
): Int {
val pivotIndex = partition(a, left, right)
val smallGroupSize = pivotIndex - left
if (k <= smallGroupSize) {
return selection(
a = a,
k = k,
left = left,
right = pivotIndex - 1
)
} else if (k == smallGroupSize + 1) {
return a[pivotIndex]
} else {
return selection(
a = a,
k = k - smallGroupSize - 1,
left = pivotIndex + 1,
right = right
)
}
}
private fun partition(
a: IntArray,
left: Int,
right: Int
): Int {
val pivotIndex = (left .. right).random()
if (pivotIndex != left) {
swap(a, pivotIndex, left)
}
val pivot = a[left]
var tempLeft = left + 1
var tempRight = right
while (true) {
while (tempLeft < right && a[tempLeft] <= pivot) {
tempLeft++
}
while (tempRight > left && a[tempRight] >= pivot) {
tempRight--
}
if (tempLeft >= tempRight) {
break
}
swap(a, tempLeft, tempRight)
tempLeft++
tempRight--
}
swap(a, left, tempRight)
return tempRight
}
private fun swap(
arr: IntArray,
a: Int,
b: Int
) {
val temp = arr[a]
arr[a] = arr[b]
arr[b] = temp
}
}
private fun main() {
val solution = SelectionExample()
var k = 1
while (true) {
val nums = intArrayOf(6, 3, 11, 9, 12, 2, 8, 15, 18, 10, 7, 14)
val a = solution.solution(
nums = nums,
k = k
)
k += 1
println(a)
if (k > nums.size) {
break
}
}
}
반응형
'Software > Algorithm' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리 (Minimum Spanning Tree) (1) | 2024.03.08 |
|---|---|
| [알고리즘] 동전 거스름돈 (Coin Change) (0) | 2024.03.07 |
| [알고리즘] 최근접 점의 쌍 찾기 (Closest Pair of Points Problem) (0) | 2024.03.06 |
| [알고리즘] 퀵정렬 (Quick Sort) (2) | 2024.02.29 |
| [알고리즘] 합병정렬 (Merge Sort) (0) | 2024.02.05 |
